트리란 ?
계층적 구조를 나타내는 자료구조이며 주로 탐색을 위해 사용된다.
*계층적 구조 : 하나의 자료 뒤에 여러자료가 연결되는 형태이다. db를 예로 들자면 1:n 관계라 할 수 있겠다.
선형적 구조 : 하나의 자료 뒤에 하나의 자료만 오는 구조이다. 배열이 대표적인 선형구조를 가지는 자료구조이다.
트리에 대한 설명 전 용어 정리부터 해보자.
트리의 용어
- 노드 : 트리의 구성요소
- 루트 : 부모가 없는 노트
- 서브트리 : 하나의 노드와 자손들로 이루어짐
- 단말노드 : 자식이 없는 노드 (leaf 노드)
- 비단말노드 : 자식을 가지는 노드
- 자식, 부모 형제, 조상 , 자손 노드
- 레벨(level) : 트리 각층의 번호
- 높이 , 깊이(height, depth) : 트리의 최대 레벨
- 차수(degree) : 노드의 자식 노드 수 , 트리의 차수는 그 트리에 있는 노드의 최대차수이다.
- 포리스트 : 트리들의 집합
* 동등한 위치에 있는 노드끼리는 간선을 가질 수 없다. 즉 사이클이 불가하다. (acyclic graph , 사이클이 없는 그래프)
* 노드 하나만 있다 해도 트리로 취급한다.
* 트리는 한 개 이상의 노드로 이루어 져야 한다. (empty tree 없다. )
일반트리
일반 트리는 자식을 두 개 이상 가질 수 있다. 만약 링크배열로 노드를 구현한다면 dinamic allocation 이 불가함으로 미리 배열크기를 지정해야 하지만 자식노드가 얼마나 올 지 모름으로 배열 크기 지정이 힘들고 노드의 구조가 복잡해 진다는 문제점이 있다.
이와 같은 이유로 효율적인 알고리즘을 위해 노드 구조를 일정하게 지정해 준다.
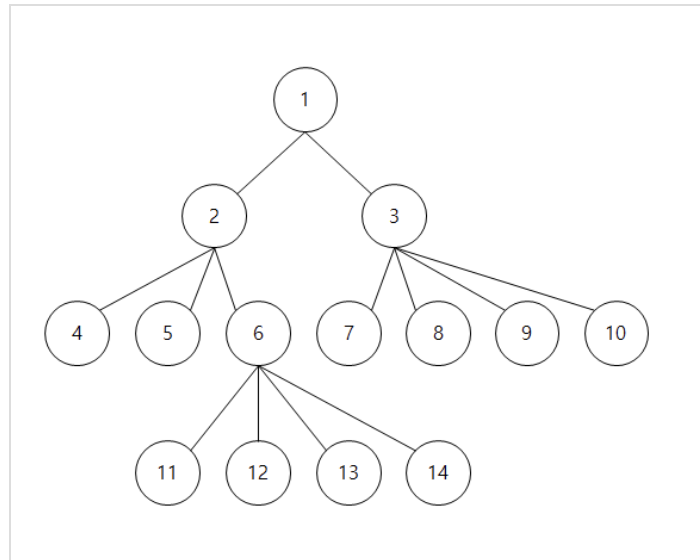
일정한 노드구조를 위해 크기 일정 방법으로 트리를 표현할 수 있다.
다음 두가지 방법을 알아보자 .
1) left child - right sibling
2) binary tree
left child - right sibling
두개의 링크필드만 가지는 노드로 트리를 구성한다.
첫번째 링크는 왼쪽 자식노드를 연결하며 두번째 링크는 다음 형제노드를 연결한다.
즉 모든 도느는 자기 왼쪽 자식만 관리하고 왼쪽 자식이 형제노드를 링크드 리스트로 관리하는 구조이다.

바이너리트리 (이진트리)
컴퓨터 응용에서 가장 많이 사용하는 트리 구조 이다.
모든 노드가 최대 두개의 서브트리를 가지고 있는 트리(모든 노드가 2개의 자식만 가짐) 이며 서브트리는 공백이 될 수 있다.
즉 서브트리는 공집합일 수 있다. (이는 공백 이진트리랑 다르다. 서브트리가 공백이 될 수 있다는 말은 자식을 안가지는 노드가 있다는 말 )
*모든 노드의 차수가 2 이하가 된다. -> 구현편리
*서브트리간의 순서가 존재한다. (왼쪽과 오른쪽 서브트리는 다르다. 왼->오 순서)
*리프노트 : 두 공백 서브트리를 가지고 있는 노드
*empty tree 가 가능하다.
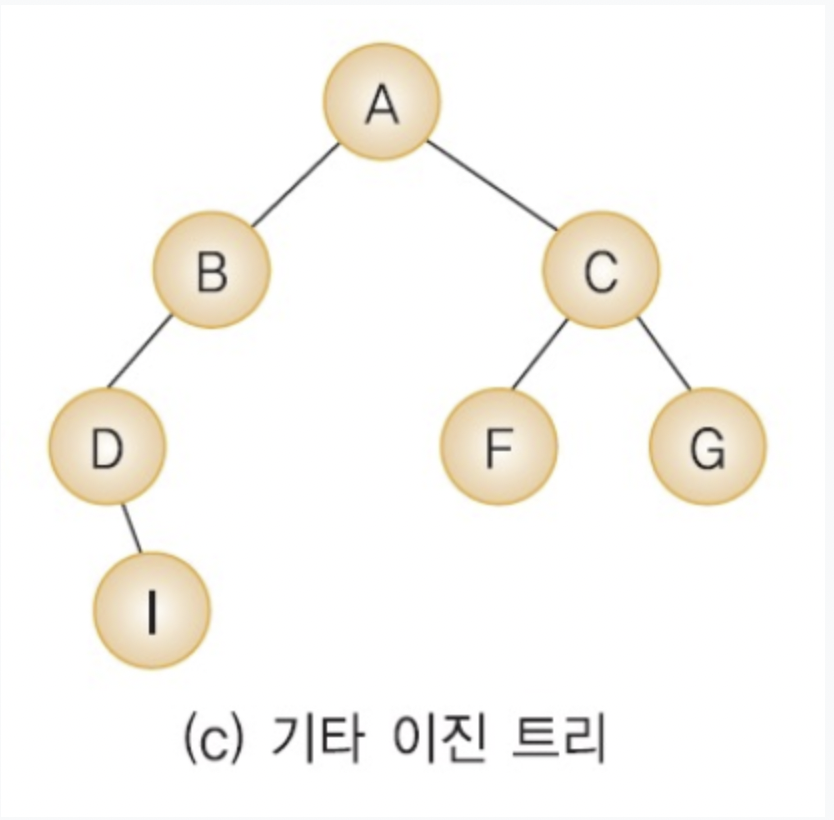
바이너리 트리와 일반 트리의 차이
1) 왼쪽 서브트리와 오른쪽 서브트리를 구분한다.
2) 공백 이진트리가 가능하다. (일반트리는 empty 될 수 없음 노드가 하나라도 있어야 한다.)
이진트리의 성질
-노드 개수가 n 개이면 간선의 개수는 n-1 이다.
(루트로 이어지는 간선은 없으니까 )
-높이가 h 이면 최대 2^h -1 개의 노드 가짐
(마찬가지로 2 단위로 늘어나는데 루트만 1개의 노드 가짐으로 1을 빼준다. )
- n 개의 노드를 가진 이진트리의 높이 log2의 (n+1) 2^n
이진트리의 분류
1) 편향 이진트리

편향 이진트리 일 경우 h 가 노드 개수와 같다.
2)포화 이진트리

포화 이진트리의 경우 최대 2^h -1 개의 노드 가짐 에서의 최대에 해당함으로 2^h -1 개의 노드를 가진다.
3) 완전 이진트리 (컴플리트 바이너리 트리)
높이가 h 일때 레벨 1 부터 h-1 까지는 모든 노드가 채워진다 (이때까지는 포화 이진 트리 , 풀 바이너리 트리)
마지막 레벨 h 에서는 노드가 왼->오 순으로 채워진다. 중간에 구멍이 나면 완전이진트리가 아닌 기타 이진트리이다.
노드번호 역시 왼쪽에서 오른쪽으로 채워진다.
포화 이진트리안에 완전 이진트리가 포함된다.
*위의 분류를 제외한 나머지는 기타 이진트리로 분류된다.
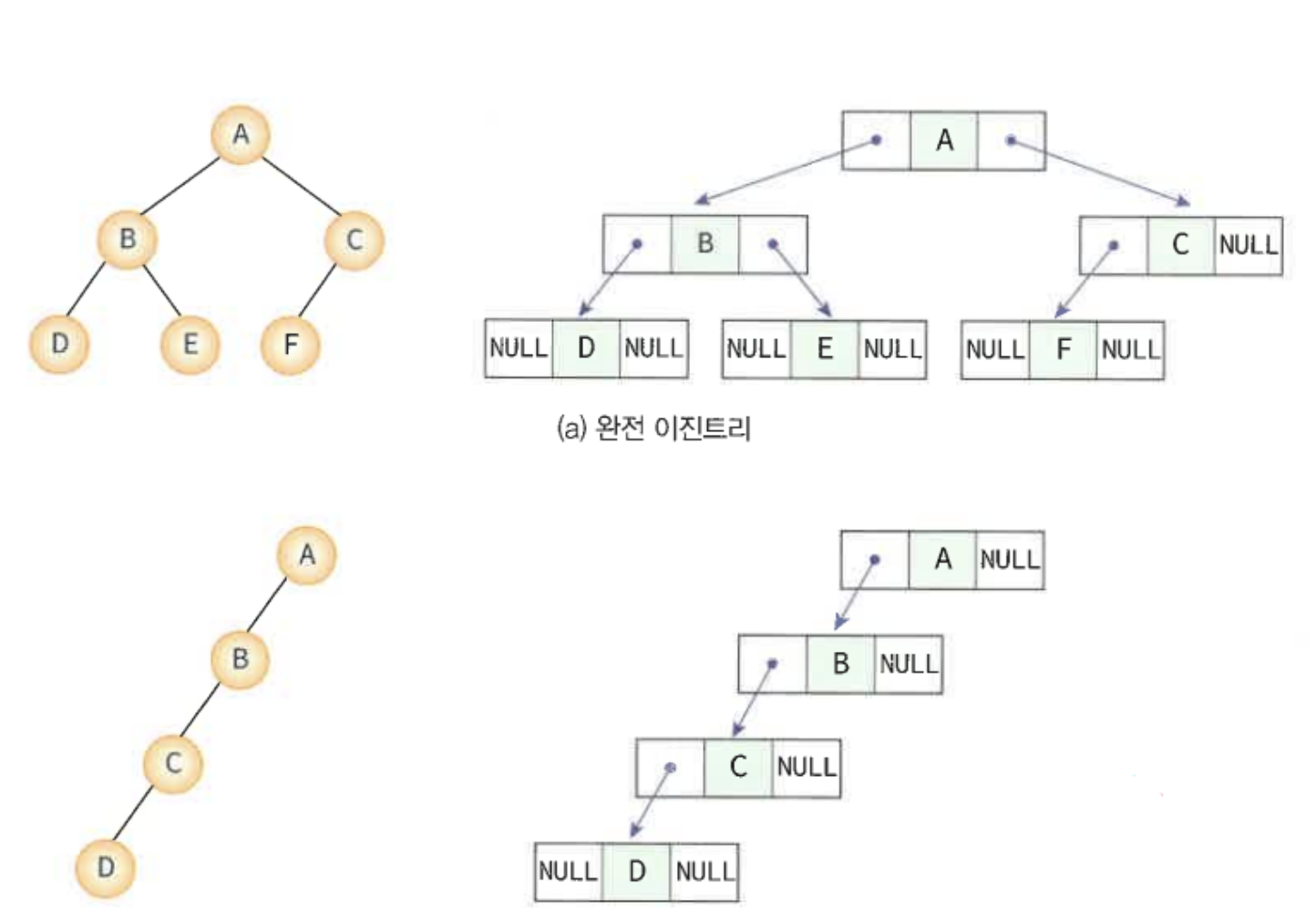
이진트리의 배열 표현법
모든 이진트리는 포화 이진트리라고 가정하고 구현한다.
각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 저장한다.

포화 이진트리나 , 완전 이진트리일 경우에는 최적이다. 구현이 쉽고 어떤 이진트리에도 사용 가능하지만

위와 같이 편향 이진트리일 경우에 배열 공간을 절반도 사용하지 못할 수 있다.
높이가 k 인 편향 이진트리는 2^k-1 개의 공간이 요구되지만 k 개의 공간만 실재로 사용한다.
또한 트리 중간에 노드의 삽입, 삭제가 일어나면 다른 노드를 이동시켜야 한다.
이진 트리의 링크표현법
부모노드가 자식노드를 가리키게 한다. 데이터필드, 링크필드 두개로 노드를 구성한다.
이진트리의 순회
순회: 트리의 노드들을 한번씩 방문하는 것
선형 자료구조에서의 순회 : 하나의 방법만 존재함
이진 트리에서의 순회 : 다양한 순회 방법이 존재한다.
1) 전위순회 : 루트-왼쪽자식-오른쪽자식
2) 중위순회 : 왼쪽자식-루트-오른쪽자식
3) 후위순회 : 왼쪽자식-오른쪽자식-루트
4) 레벨 순회 : 큐를 사용하여 노드를 왼쪽부터 오른쪽으로 검사한다.
순회 알고리즘은 노드에서 구현 할 수도 있고 트리에서 구현 할 수도 있다.
노드에서 구현
void inorder()
{
if( left != NULL ) left->inorder();
printf( " [%d] ", data);
if( right!= NULL ) right->inorder();
};
void preorder(){
printf( " [%d] ", data);
if( left != NULL ) left->preorder();
if( right!= NULL ) right->preorder();
};
void postorder(){
if( left != NULL ) left->postorder();
if( right!= NULL ) right->postorder();
printf( " [%d] ", data);
};
노드 class 의 멤버함수로 순회함수를 구현해 주었기 때문에 left-> inorder() 로 left 가 들어있는 링크(포인터) 에서 (노드가 들어있겠죠?) inorder() 함수를 재귀 호출한 것을 볼 수 있다.
마찬가지로 객체.getdata() 의 방식이 아닌 바로 data 로 해당 객체의 필드를 쓰고 있는 것 을 볼 수 있다.
*해당 노드를 기준으로 left , Right 로 이동하기 때문에 따로 노드 객체를 받지 않는다. 해당 노드가 루트 노드면 루트부터 tirverse 하게 되는것, 아니라면 해당 노드를 기준으로 triverse( 중간에 있는 노드에서 triverse 도 가능하다는 말이다 )
tree class 에서의 구현
public:
//아무것도 안넣으면 root 부터, 아니면 해당 노드부터
int getCount() { return isEmpty() ? 0 : getCount(root); }
int getLeafCount(){ return isEmpty() ? 0 : getLeafCount(root); }
int getHeight() { return isEmpty() ? 0 : getHeight(root); }
void inorder() { printf("\n inorder: "); inorder(root); }
void preorder() { printf("\n preorder: "); preorder(root); }
void postorder(){ printf("\n postorder: "); postorder(root); }
private:
void inorder(BinaryNode *node) { //함수의 예상치 못한 동작 막음 이거 public 이면 root 에서부터 동작 x
if( node != NULL ) {
if( node->getLeft() != NULL ) inorder(node->getLeft());
printf( " [%c] ", node->getData());
if( node->getRight()!= NULL ) inorder(node->getRight());
}
}
void preorder(BinaryNode *node) {
if( node != NULL ) {
printf( " [%c] ", node->getData());
if( node->getLeft() != NULL ) preorder(node->getLeft());
if( node->getRight()!= NULL ) preorder(node->getRight());
}
}
void postorder(BinaryNode *node) {
if( node != NULL ) {
if( node->getLeft() != NULL ) postorder(node->getLeft());
if( node->getRight()!= NULL ) postorder(node->getRight());
printf( " [%c] ", node->getData());
}
}
코드를 확인해 보자. node class 에서 구현한 것과 달리 inorder함수가 private , public 으로 오버로딩 되어 두번 짜져 있다. 로직상 private 함수의 파라미터로는 무조건 root 노드만 들어가게 구현되어 있음으로 중간노드 에서의 순회는 불가하다.
또한 tree 클래스 임으로 필드에 직접 접근이 불가하다. 따라서 node -> getLeft() 나 node->getData() 같이 게터세터 함수로 필드를 가져온 것을 볼 수 있다.
*모든 함수에 if(node->getLeft()!= NULL) 과 같이 노드의 링크필드가 null 인지 확인하고 순회하는 if 문이 걸려있다. 이 조건을 걸어주지 않더라도 재귀호출시 if( node != NULL ) 에 걸리기 때문에 이 부분은 제외해도 정상 작동한다.
// 레벨 순회 연산
void levelorder() {
printf("\nlevelorder: ");
if( !isEmpty() ) {
CircularQueue q;
q.enqueue( root );
while ( !q.isEmpty() ) {
BinaryNode* n = q.dequeue();
if( n != NULL ) {
printf(" [%c] ", n->getData());
q.enqueue(n->getLeft ());
q.enqueue(n->getRight());
}
}
}
printf("\n");
}
위의 중위전위후위 순회법은 root 부터 시작되어야 한다. 재귀호출은 파라미터로 특정 node를 받아 그 자리에서 부터 시작하는 순회가 가능하기에 private 로 구현해 주었다. 레벨 순회는 파라미터로 아무것도 받지 않고 큐를 사용하여 순회함으로 public 으로 구현되어 있다.
해당 함수 안에서 CircularQueue 객체를 하나 선언해 준다. 루프 시작전 root 를 넣어두고 큐가 빌때까지를 탈출조건으로 while 문을 돌린다. 루트부터 시작해 왼쪽 오른쪽 노드를 큐에 삽입하며 순서대로 뽑아서 마찬가지로 해당 노드의 왼쪽 오른쪽 노드를 삽입하는 과정을 반복한다. 이후 디큐 한 노드가 null 이 되면 삽입을 멈추고 종료한다.
class CircularQueue
{
int front;
int rear;
BinaryNode* data[MAX_QUEUE_SIZE];기존 코드와 바뀐 부분 : CircularQueue 의 필드중 data 필드를 BinaryNode 의 * 타입으로 바꾸었다.
//디렉터리 용량 계산
int calcSize() { return calcSize(root); }
int calcSize(BinaryNode *node) {
if( node == NULL ) return 0;
return node->getData() + calcSize(node->getLeft()) + calcSize(node->getRight());
}후위순회 사용하는 예시 . 디렉터리 용량을 계산하는 함수이다. 이렇게 이진트리는 파일 시스템에서 많이 쓰인다.
이진트리 연산
노드개수
//노드 개수 구하기
public:
int getCount() { return isEmpty() ? 0 : getCount(root); }
int getCount(BinaryNode *node) {
if( node == NULL ) return 0;
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}전체 노드 개수를 구하는 함수이다.
empty 여부를 확인하고 오버로딩 된 함수를 호출한다.
node 가 null 일 경우( 더이상 내려갈 노드가 없는경우) 0을 반환하고 그렇지 않으면 재귀 호출로 1+ node의 왼쪽 자식의 포인터를 함수에 다시 넣는 방식으로 동작한다.
*파라미터 없이 호출하면 루트 기준으로 getcount 한다. 저자가 재귀 호출을 사용했음에도 불구하고 해당 코드를 public 으로 구현한것이 의문 이었는데 중간 노드를 기준으로도 노드 개수를 구할 수 있게 하기위해서 였던 것 같다.
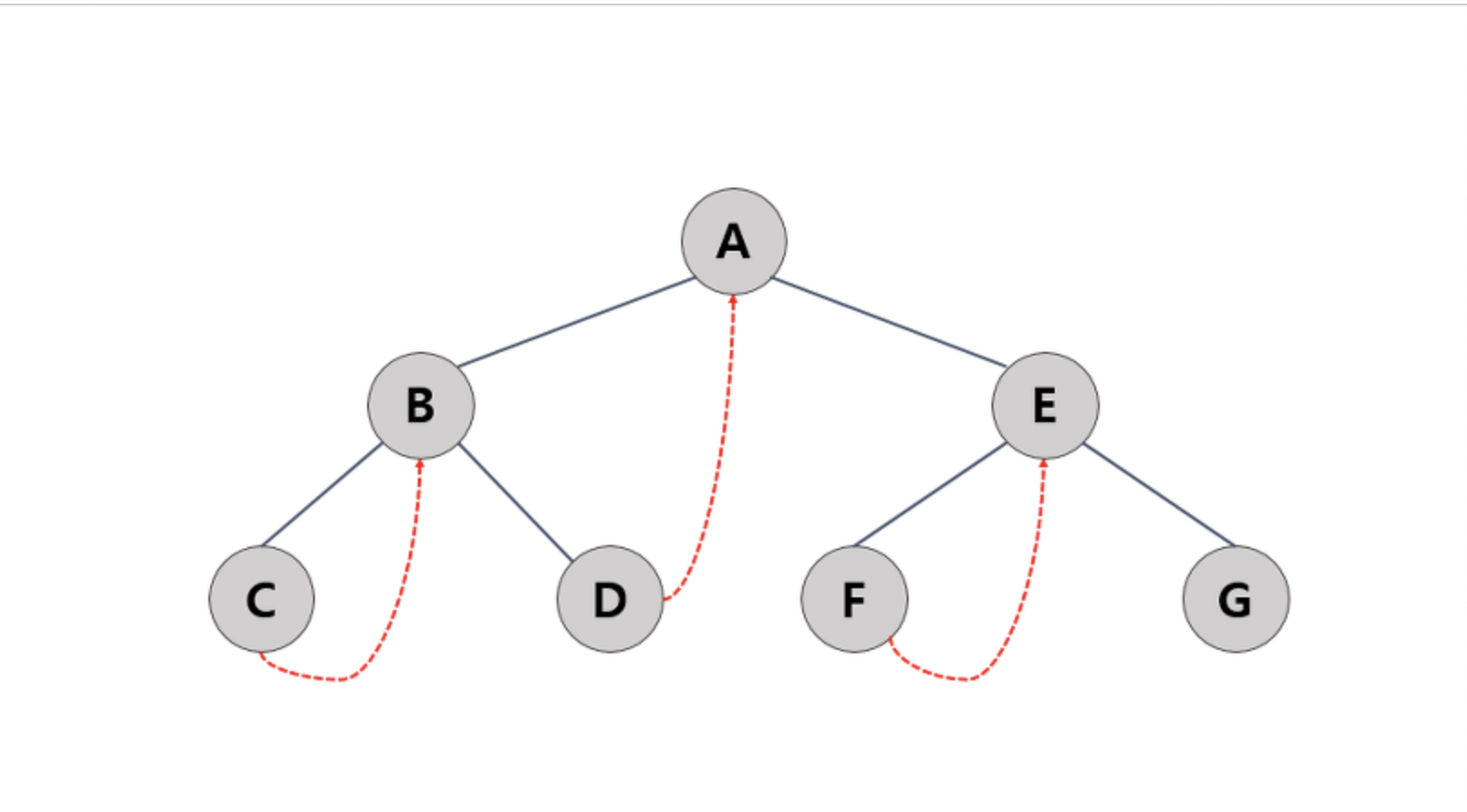
설명을 위해 그림을 그려보자.
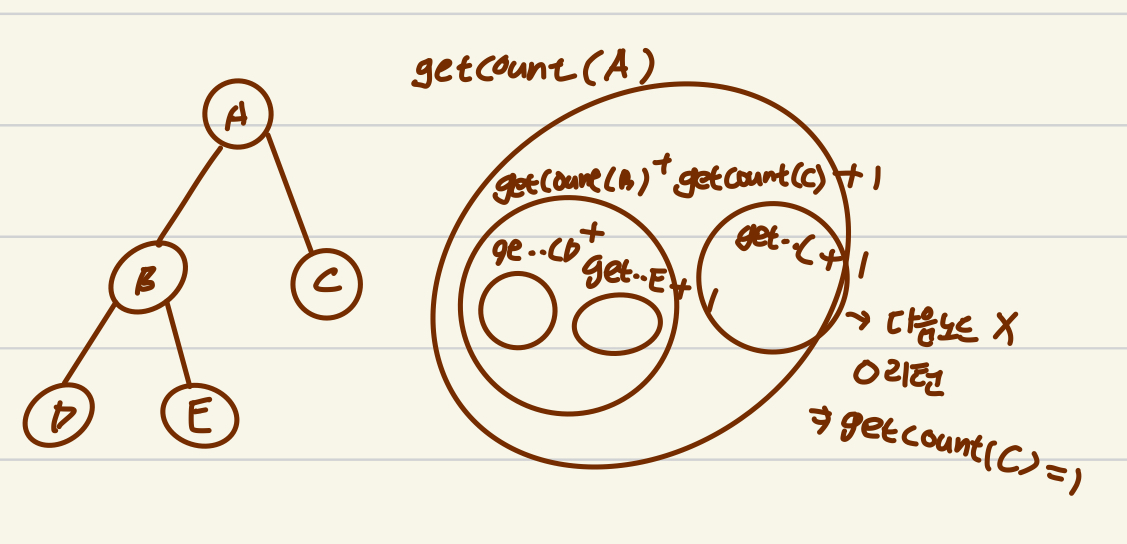
다음 트리를 보고 노드 개수를 구하는 코드를 적용해보자. 먼저 getcount(A) 루트노드인 A가 들어올 것이고 null 이 아님으로 1+ getcount(B) + getcoutn(C)+1 을 리턴할것이다. 여기서 getcount(B) 와 getcount(C) 는 다시 함수를 재귀호출 함으로 결론적으로
getcount(A) = getcount(B) + getcoutn(C)+1 = (getcount(D)+getcount(E)+1) + (getcount(C)) + 1 이 된다.
단말노드 개수
public:
int getLeafCount(){ return isEmpty() ? 0 : getLeafCount(root); }
//단말노드 개수 구하기
int getLeafCount(BinaryNode *node) {
if( node == NULL ) return 0;
if( node->isLeaf() ) return 1;
else return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}위의 그림을 통해 재귀 호출의 성질을 충분히 설명 했음으로 자세한 설명은 생략하겠다.
isLeaf() 함수는 node class의 필드함수로 getLeft() == null && getRight() == null 인 경우에 true 를 반환하도록 구현 된 함수다.
높이
public:
int getHeight() { return isEmpty() ? 0 : getHeight(root); }
//트리 높이 구하기
int getHeight(BinaryNode *node) {
if( node == NULL ) return 0;
int hLeft = getHeight(node->getLeft());
int hRight = getHeight(node->getRight());
return (hLeft>hRight) ? hLeft+1 : hRight+1;
}위와 비슷한 방식의 리커젼 코드이다. 다른 부분은 return 부분에서 재귀호출을 하는 것이 아닌 변수에서 재귀 호출 한다음 return 에서 크기를 비교하는 것이다.
* 해당 코드의 모든 리커젼 코드는 null 일때 무언가 값을 반환하고 그 값을 기준으로 차례차례 위로 올라오는 모양새다. 이 부분을 잘 이해하면 차례 차례 올라오면서 개수나 높이를 구할 수 있다.
수식 이진 트리
산술식을 트리 형태로 표현한 것이다.
비단말 노드는 연산자, 단말노드는 피연산자로 구성된다.
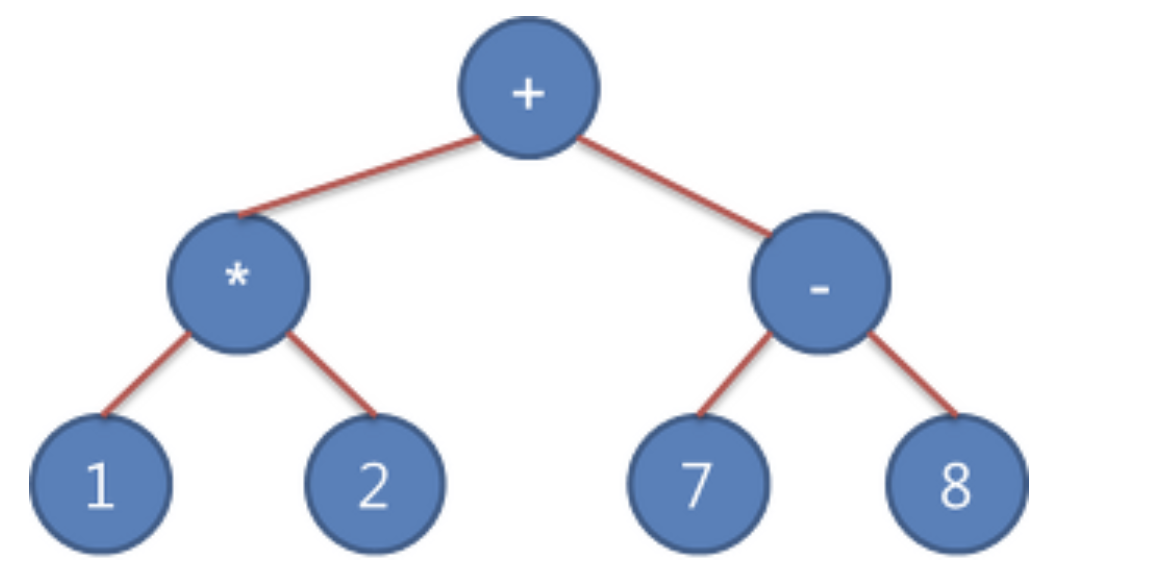

여러 순회중 후위순회를 사용해서 구현해보자.
public:
//수식트리 함수
int evaluate() { return evaluate(root); }
int evaluate(BinaryNode *node) {
if( node == NULL ) return 0;
if( node->isLeaf() ) return node->getData();
else {
int op1 = evaluate(node->getLeft());
int op2 = evaluate(node->getRight());
switch(node->getData()){
case '+': return op1+op2;
case '-': return op1-op2;
case '*': return op1*op2;
case '/': return op1/op2;
}
return 0;
}
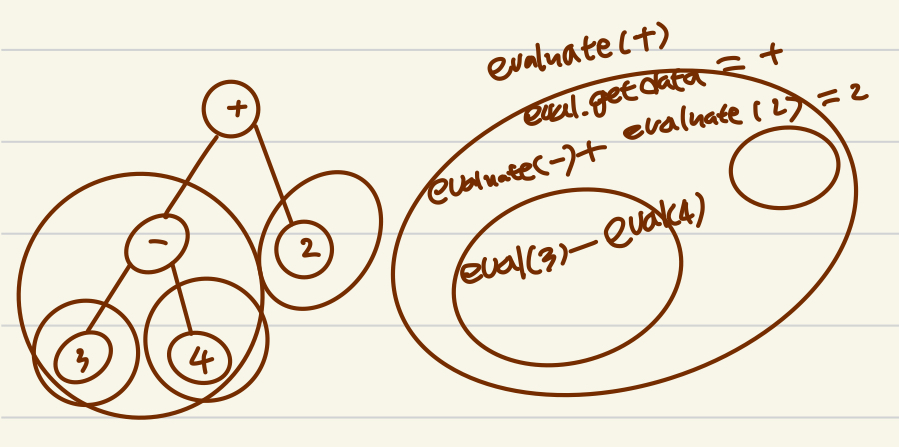
}마찬가지로 루트를 넣어서 함수를 시작해 준다. 위의 전체 예시에서 루트를 넣는 부분은 루트 객체 자체를 넣는것이 아닌 루트 객체를 가리키는 포인터를 넣는 것임을 잊지 말자.
이 함수 역시 마지막 리프노드만 데이터를 리턴한다. 위의 그림, 마주르카 인형처럼 겹겹이 쌓여서 더해진다고 생각하면 편하게 이해할 수 있을 것이다.
스레드 이진 트리 (TBT)
연결리스트로 표현한 이진 트리의 문제점
n개의 노드를 가진 이진트리의 총 링크수는 2n 개이다.
하지만 실재로 사용되는 링크수는 n-1 개이다 ( 리프노드는 링크를 가지지 않기 때문)
널 링크수가 n+1 개인 셈이다.
스레드 이진트리는 이러한 문제를 해결하기 위해 널 링크들을 낭비하지 않고 스레드를 저장해 활용한다.
스레드 : 트리의 다른 노드에 대한 포인터
즉 리프 노드의 right 부분에는 중위 순위에서 중위 후속자(중위순회를 할때 해당노드 다음 차례에 올 노드를 말함) 에 대한 포인터를 저장하고 left 부분에는 중위 선행자(중위순회에서 해당노드 이전차례였던 노드를 말함) 에 대한 포인터를 저장한다.
*교제코드에선 중위선행자 부분을 생략하였다.
이런식으로 트리의 null 링크를 이용하여 리커젼 없이 순환호출 하며 노드를 순회할 수 있다.
*bThread 필드가 필요하다. 자식포인터인지 스레드인지를 알아야! 스레드이면 false 아니면 true 를 리턴하는 방식으로 구현해 주어야 한다. 이때 false 인 경우는 스레드가 들어있거나 null (중위순회의 끝노드) 인 경우이다.
class ThreadedBinNode
{
protected:
int data;
ThreadedBinNode *left;
ThreadedBinNode *right;
public:
bool bThread;
ThreadedBinNode( int val=0, ThreadedBinNode *l=NULL, ThreadedBinNode *r=NULL, bool bTh=false)
: data(val), left(l), right(r), bThread(bTh) { }
int getData () { return data; }
void setRight(ThreadedBinNode *r) { right= r; }
ThreadedBinNode* getLeft () { return left; }
ThreadedBinNode* getRight() { return right; }
};스레드 바이너리 노드 class 이다. bThred 필드가 추가된 것을 볼 수 있다.
#pragma once
#include "ThreadedBinNode.h"
class ThreadedBinTree
{
ThreadedBinNode* root;
public:
ThreadedBinTree(): root(NULL) { }
~ThreadedBinTree() { }
void setRoot(ThreadedBinNode* node) { root = node; }
ThreadedBinNode* getRoot() { return root; }
bool isEmpty() { return root==NULL; }
void threadedInorder() {
if( !isEmpty() ) {
printf("스레드 이진 트리 : ");
ThreadedBinNode *q = root;
while (q->getLeft()) q = q->getLeft();//처음만 왼쪽노트 쭉 찾음
do {
printf("%c ", q->getData());
q = findSuccessor(q); //오른쪽노드 검사
} while(q);
printf("\n");
}
}
ThreadedBinNode* findSuccessor(ThreadedBinNode* p){
ThreadedBinNode *q = p->getRight(); //오른쪽 노드에 대한 검사
if( q==NULL || p->bThread ) return q; //오른쪽노드가 쓰레드일경우 오른쪽노드 리턴
while( q->getLeft() != NULL ) q = q->getLeft(); //자식일경우 그 자식의 왼쪽자식 있는지 검사
return q; //왼쪽자식 있으면 왼쪽으로 가서 리턴
}
};사진 출처
https://justicehui.github.io/hard-algorithm/2021/03/22/tree-binary-transform/
트리 이진 변환
서론 이진 트리는 일반적인 트리에 비해 효율/구현에서 많은 이점을 갖고 있습니다. 자식의 개수가 2개 이하로 일정하고, 트리의 순회 순서를 강제하기 쉬우며, 모든 정점의 차수가 3 이하라는
justicehui.github.io
https://yangdongjae.github.io/computerscience/Tree_Left_Child_Right_Sibling/
[자료구조,Python] 파이썬으로 만들어보는 Tree(Left Child- right Sibling)
[자료구조,Python] 파이썬으로 구현하는 트리(Tree_Left Child- right Sibling) 자료구조
yangdongjae.github.io
https://velog.io/@xx0hn/CS-DataStructure-Tree
[ CS / DataStructure ] Tree
트리는 스택이나 큐와 같은 선형 구조가 아닌 비선형 구조이다. 트리는 계층적 관계를 표현하는 자료구조로 표현에 집중한다. 무엇인가를 저장하고 꺼내야 한다는 사고에서 벗어나 트리라는 자
velog.io
https://velog.io/@away0419/Binary-Tree%EC%9D%B4%EC%A7%84-%ED%8A%B8%EB%A6%AC
Binary Tree(이진 트리)
각 노드가 자식노드를 2개 이하로 가진 트리포화 이진 트리\-모든 레벨이 꽉 찬 이진 트리 완전 이진 트리\-위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 이진 트리정 이진 트리\-모든 노
velog.io
https://velog.io/@heesun729/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC
[자료구조] 트리(1) - 링크 표현법, 순회
8.1 트리 > 리스트, 스택, 큐 등은 선형 구조 이지만 트리는 계층적인 구조를 나타내는 비 선형구조다. 제약조건이 있는 그래프(사이클이 없는 연결 그래프 ✨ 트리의 응용 분야: 계층적인 조직,
velog.io
https://cs-ssupport.tistory.com/150
[Data Structure] 이진 트리 : 수식 트리
수식 트리 - 산술 연산자(+, -, *, /), 피연산자로 구성 - 피연산자 = 단말노드 - 산술 연산자 = 비단말노드 - 각 루트노드들은 산술 연산자이기 때문에 루트보다 자식 노드(피연산자)들을 먼저 방문
cs-ssupport.tistory.com
https://mattlee.tistory.com/29
<스레드 이진트리> 기본개념과 알고리즘
# 스레드 이진트리 // 이 글은 드래그 및 복붙이 되지 않습니다. 소스파일은 하단에 첨부되어 있습니다. 이진트리 순회는 순환호출을 사용한다. 하지만, 순환호출은 반복문에 의해 훨씬 비효율적
mattlee.tistory.com
'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조]그래프 (2) | 2024.10.22 |
|---|---|
| [자료구조] 우선순위큐 (1) | 2024.10.21 |
| [자료구조] 이진탐색트리 (4) | 2024.10.20 |