[자료구조]그래프
그래프란?
연결돼있는 객체 간 관계를 표현하는 자료구조
ex) 트리, 지하철 노선도 , 노드와 노드 사이를 연결선으로 표현할 수 있으면 그래프
오일러문제
다리를 한번만 건너서 처음 출발했던 장소로 돌아오는 문제
위치 : 정점
다리 : 간선
오일러 정리 : 모든 정점에 연결된 간선의 수가 짝수면 오일러 경로가 존재한다. ( 처음 출발한 장소로 돌아올 수 있다. )
그래프 정의
그래프 G = (V, E)
- 정점(노드, vertex) : 여러가지 특성을 가질 수 있는 객체 의미, V(G) 그래프 G의 정점들의 집합, 공백 x
- 간선(링크, edge) : 정점들 간의 관계 의미 , E(G) 그래프 G의 간선들의 집함, 공집합 0
*엣지가 하나도 없어도 그래프 될 수 있다.
동일한 그래프?
- 그래프는 오직 정점과 간선의 집합, 시작적 표현으로 판단 x
그래프의 종류
간선의 종류에 따라
1) 무방향 그래프 : 간선을 통해서 양방향으로 갈 수 있음 , (A,B) =(B,A)
2) 방향 그래프 : 간선을 통해서 한쪽 방향으로만 갈 수 있음 <A,B> != <B,A>
가중치 그래프 : 네트워크 라고도 함, 간선에 비용이나 가중치가 할당된 그래프
부분그래프 : 정점의 집합 V(G) 와 간선의 집합 E(G) 의 부분집합으로 이루어진 그래프

그래프 표현의 예
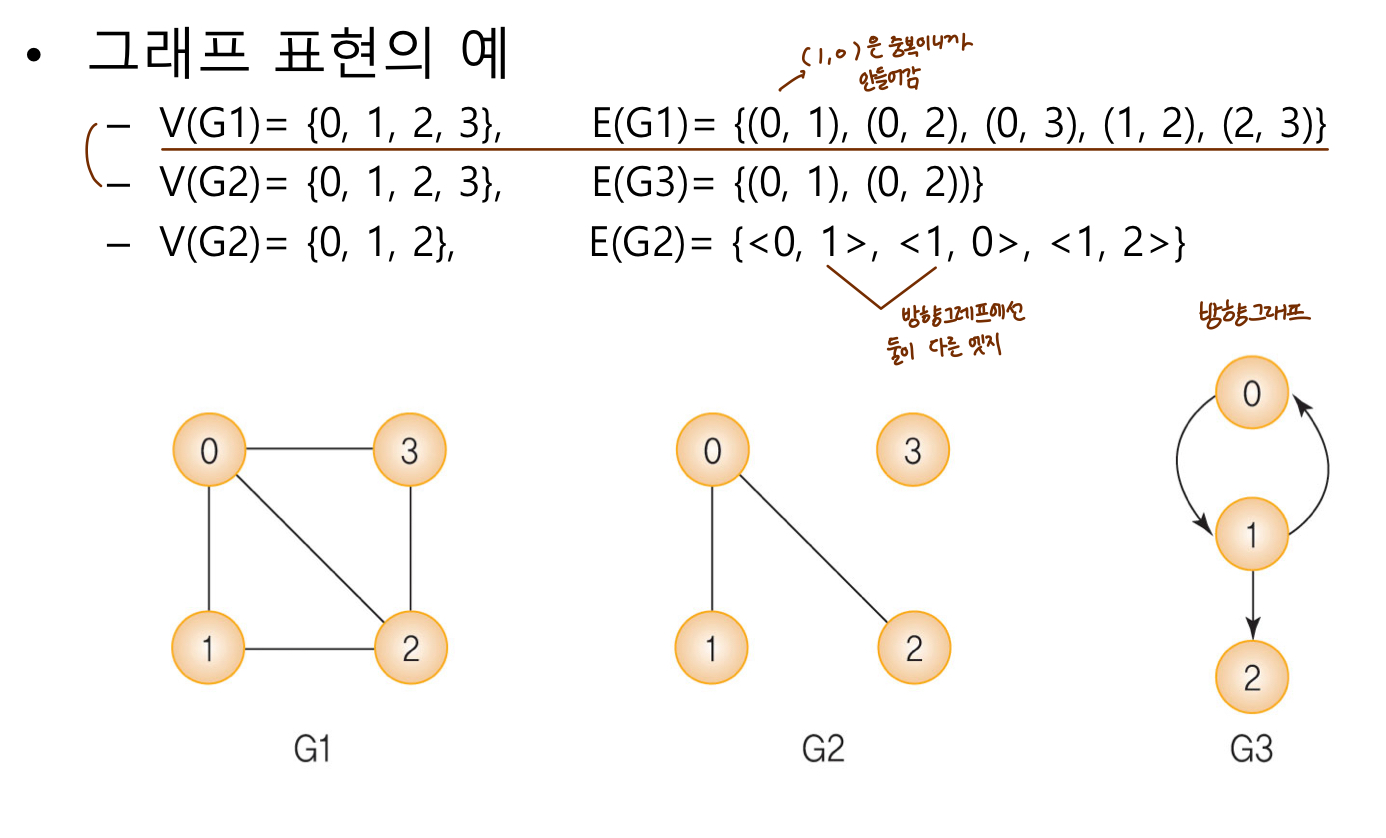
그래프의 용어
인접 정점
- 하나의 정점에서 간선에 의해 직접 연결된 정점
- G1 에서 정점 0의 인접 정점
차수
- 하나의 정점에 연결된 다른 정점의 수
- 무방향 그래프 : g1 에서 정점 0 의 차수 3 , 차수의 합은 간선 수의 2배이다.
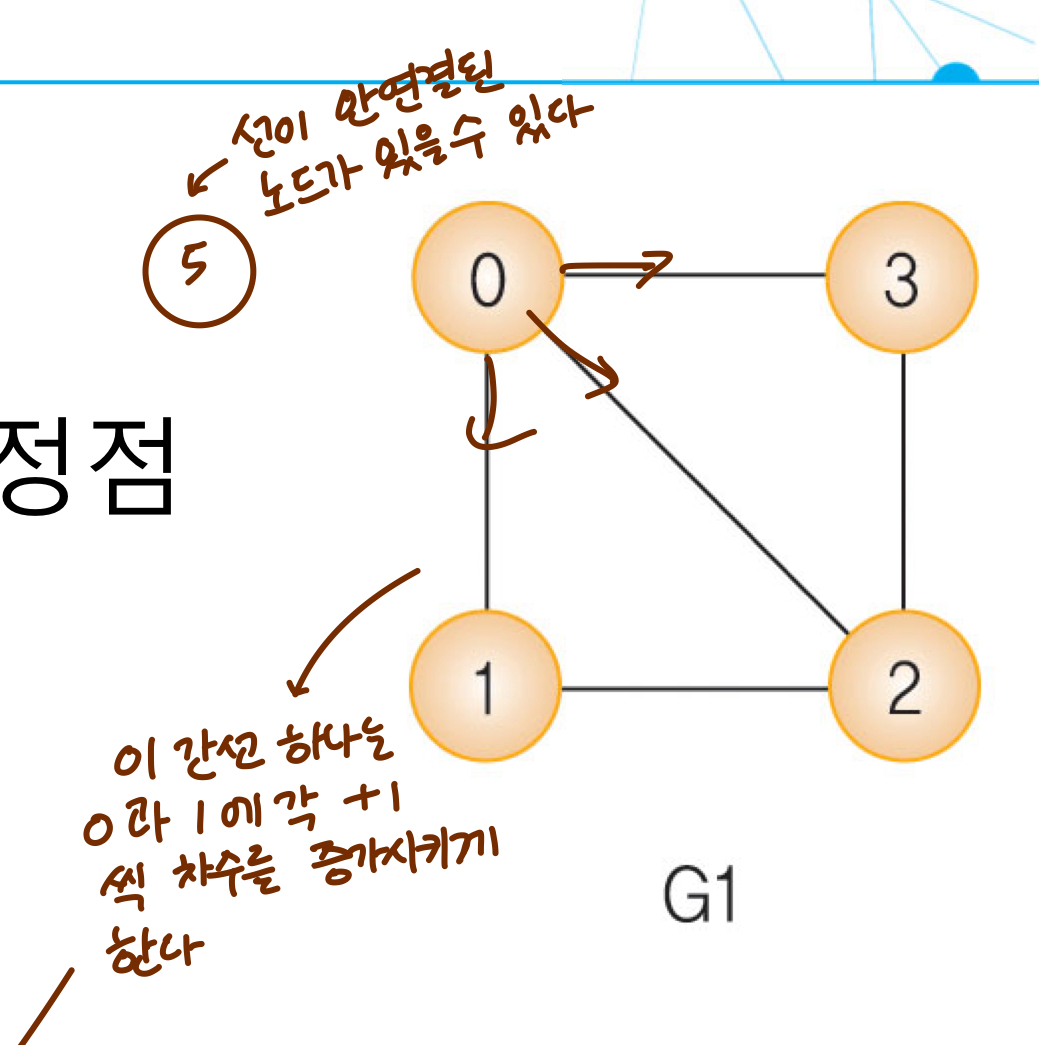
- 방향 그래프 : 진입차수, 진출차수 , 모든 진입(진출) 차수의 합은 간선의 수

경로의 길이
경로를 구성하는데 사용된 간선의 수
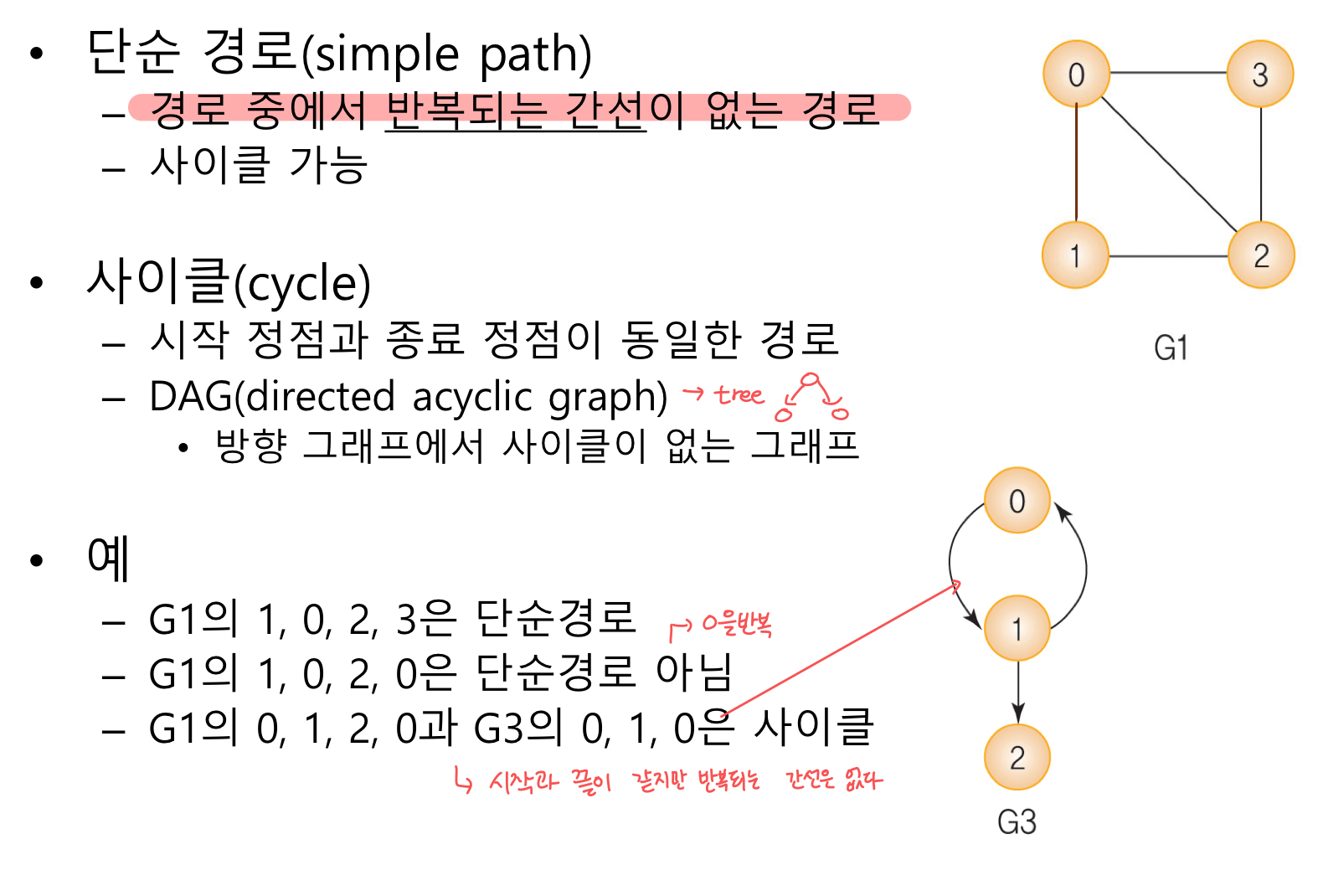
단순경로
- 경로 중에서 반복되는 간선이 없는 경로
- 사이클 가능
사이클
- 시작 정점과 종료 정점이 동일한 경로
- DAG(directed acyclic graph) : 방향 그래프에서 사이클이 없는 그래프 ex) tree
연결 그래프
- 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 무방향 그래프 (즉 간선이 없는 노드가 없음) 그래프에서 어떤 정점에서 다른 정점까지 갈 수 있는 경로가 존재하면 두 정점은 연결되었다고 한다.
- 어느 한 정점에서부터 다른 어떤 정점으로의 경로 존재

트리
- 그래프의 특수한 형태로서 사이클을 가지지 않는 연결 그래프

완전 그래프
- 최대 수의 간선을 가진 그래프
- 모든 정점이 연결되어 있는 그래프
- 간선의 수는 무방향일 때 nC2 = n(n-1)/2 서로다른 n개의 원소에서 순서없이 2개씩 꺼내는 경우의 수
- 방향그래프일때 nP2 서로다른 n 개의 원소에서 순서 있게 2개씩 꺼내는 경우의 수

인접행렬로 그래프 표현 (adJacent matrix)
n*n 의 인접행렬 M 을 이용
- 간선 (i, j) 가 그래프에 존재 , M[i][j] =1
- 그렇지 않으면 M[i][j] =0
- 대각선 성분은 모두 0
- 무방향 그래프 (인접행렬이 대칭)

인접행렬을 이용한 그래프 구현
#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#define MAX_VTXS 256
class AdjMatGraph
{
protected:
int size;
char vertices[MAX_VTXS];
int adj[MAX_VTXS][MAX_VTXS];
public:
AdjMatGraph( ) { reset(); }
~AdjMatGraph() { }
char getVertex(int i) { return vertices[i]; }
int getEdge(int i, int j) { return adj[i][j]; }
void setEdge(int i, int j, int val) { adj[i][j] = val; }
bool isEmpty() { return size==0; }
bool isFull() { return size>=MAX_VTXS; }
void reset() {
size=0;
for(int i=0 ; i<MAX_VTXS ; i++ )
for(int j=0 ; j<MAX_VTXS ; j++ )
setEdge(i,j,0);
}
void insertVertex( char name ) {
if( !isFull() ) vertices[size++] = name;
else printf("Error: 그래프 정점 개수 초과\n");
}
void insertEdge( int u, int v ) {
setEdge(u,v,1);
setEdge(v,u,1);
}
void display( FILE *fp = stdout) {
fprintf(fp, "%d\n", size);
for( int i=0 ; i<size ; i++ ) {
fprintf(fp,"%c ", getVertex(i));
for( int j=0 ; j<size ; j++ )
fprintf(fp, " %3d", getEdge(i,j));
fprintf(fp,"\n");
}
}
*여기서 insertVerdex 시 vertices[size++] = name 에 의문을 느낄 수 있다. 정점이 추가됨으로 인접행렬 크기가 추가돼야 한다는 것이다. but 인접행렬은 배열이다 처음 만들때 size 는 정해놨음으로 이미 256*256 메모리가 잡혀있고 우리가 vertex 를 넣지 않으면 그 공간은 안쓰는 공간이 될 뿐이다.
그래프를 파일로 관리
g.store( "graph.txt" );
g.reset();
g.load( "graph.txt" );
printf("인접 행렬로 표현한 그래프 (파일:graph.txt)\n");
g.display();
//insertdege 하기 귀찮아서 만든거 , 필요하면 load 해서 쓰자
인접행렬을 미리 그려놓은 txt 를 load 해서 사용하자는 것이다. insertadge 하기 귀찮아서 만들어 둔 메트릭스이다.
void load(const char *filename) {
FILE *fp = fopen(filename, "r");
if( fp != NULL ) {
int n;
fscanf(fp, "%d", &n);
for(int i=0 ; i<n ; i++ ) {
char str[80];
int val;
fscanf(fp, "%s", str);
insertVertex( str[0] );
for(int j=0 ; j<n ; j++){
fscanf(fp, "%d", &val);
if( val != 0 )
insertEdge (i,j);
}
}
fclose(fp);
}
}
void store(const char *filename) {
FILE *fp = fopen(filename, "w");
if( fp != NULL ) {
display( fp );
fclose(fp);
}
}
w 모드로 파일을 열어 fp 에 해당 파일에 있는 내용을 display 해 준다. 만약 filename 이 들어오지 않으면 stdout 으로 콘솔에 출력된다.
인접리스트로 그래프 표현
인접리스트
- 각 정점이 연결리스트를 가짐
- 인접한 정점들을 연결리스트로 표현
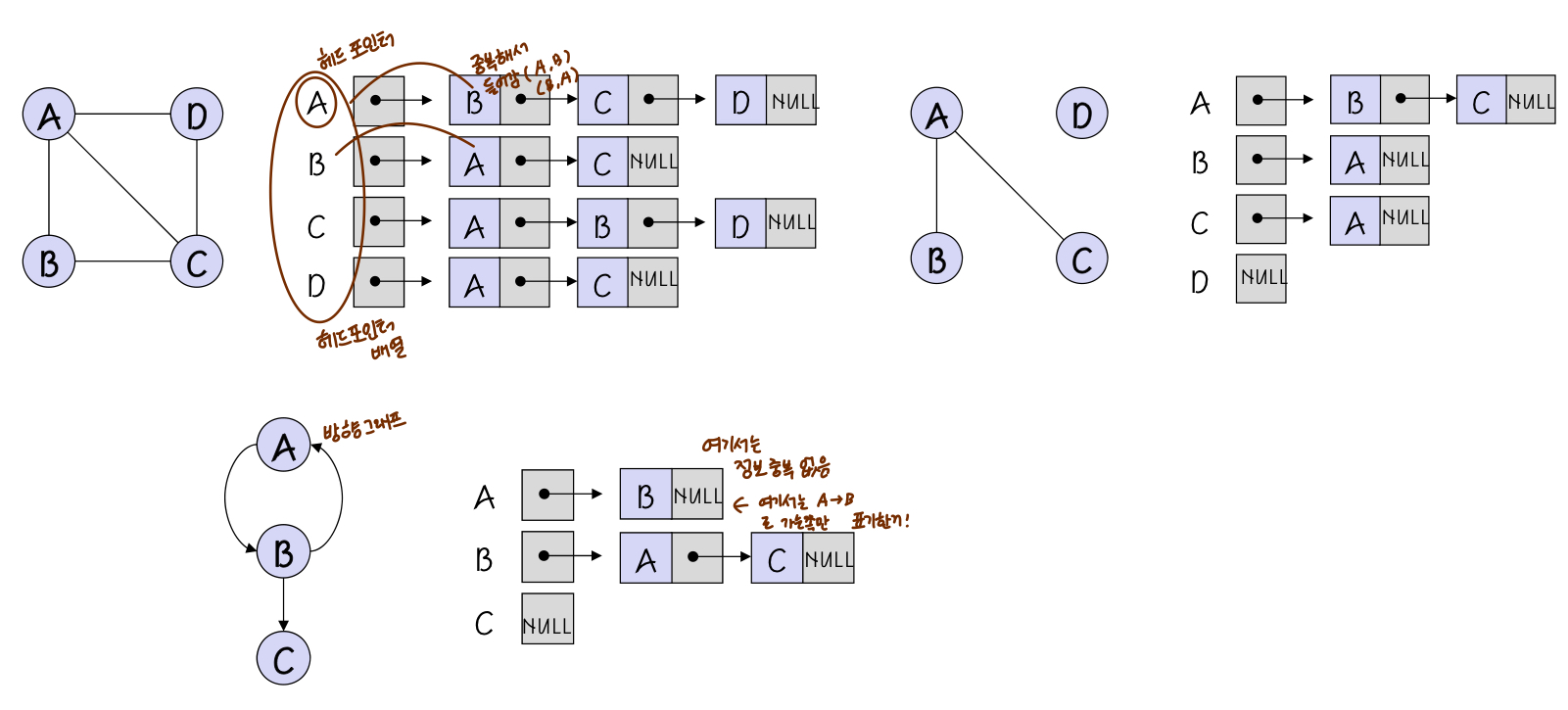
코드로 인접리스트를 구현해보자.
#pragma once
#include <stdio.h>
class Node
{
protected:
int id; // 정점의 id
Node* link; // 다음 노드의 포인터
public:
Node( int i, Node *l=NULL ) : id(i), link(l) { }
~Node(void) {
if( link != NULL )
delete link;
}
int getId() { return id; }
Node* getLink() { return link; }
void setLink(Node* l) { link = l; }
};
이때 ~Node() 부분에서 if(link != null) 일때 link; 가 연쇄적으로 삭제된다.
class AdjListGraph
{
int size; //정점개수
char vertices[MAX_VTXS]; //정점 정보 (헤드포인터의 data)
Node* adj[MAX_VTXS]; //각 정점의 인접 리스트 (헤드포인터 배열)
public:
AdjListGraph(void) : size(0) { }
~AdjListGraph(void){ reset(); }
void reset(void) {
for( int i=0 ; i<size ; i++ )
if( adj != NULL ) delete adj[i];
size = 0;
} //헤드포인터만 삭제되면 연쇄적으로 삭제된다.
bool isEmpty() { return (size==0); }
bool isFull() { return (size>=MAX_VTXS); }
char getVertex(int i) { return vertices[i]; }
void insertVertex( char val ) { //정점 삽입
if( !isFull() ) {
vertices[size] = val; //정점넣고
adj[size++] = NULL; //다음 정점을 가리킬게 없으니까 null 넣음
}
else printf("Error: 정점 개수 초과\n");
}
void insertEdge( int u, int v) { //u에다 v 넣는것
adj[u] = new Node (v, adj[u]); //맨 앞에 삽입됨으로 기존 adj[u]가 가리키던 링크 가리킴
adj[v] = new Node (u, adj[v]); //무방향임으로 adj[v]에도 같은 작업
}
void display( ) {
printf("%d\n", size);
for( int i=0 ; i<size ; i++ ) {
printf("%c ", getVertex(i));
for( Node *v=adj[i] ; v != NULL ; v=v->getLink() )
printf(" %c", getVertex(v->getId()) );
printf("\n");
}
}
그래프 탐색
그래프의 가장 기본적인 연산
- 시작 정점부터 차례대로 모든 정점을 한 번씩 방문한다.
- 깊이 우선 탐색 (DFS)
- 너비 우선 탐색 (BFS)
깊이 우선 탐색 (DFS)
DFS : depth-first search
- 한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아와서 다시 탐색 진행
- 되돌아가기 위해서는 스택 필요 (순환함수 호출로 묵시적 스택 사용)
DFS 구현 : 인접행렬
#pragma once
#include "AdjMatGraph.h"
#include "CircularQueue.h"
class SrchAMGraph : public AdjMatGraph
{
bool visited[MAX_VTXS];
public:
void resetVisited() {
for( int i=0 ; i<size ; i++ )
visited[i] = false;
}
bool isLinked(int u, int v) { return getEdge(u,v) != 0; }
// 깊이 우선 탐색 함수
void DFS( int v) {
visited[v] = true;
printf("%c ", getVertex(v));
for( int w=0 ; w<size ; w++)
if( isLinked(v,w) && visited[w]==false )
DFS( w );
}
방문 정점의 visited 를 true 로 바꿔주고 정점을 print 해 준다. 인접행렬의 size 만큼 루프를 돌면서 해당 정점과 링크되어 있는 정점이 있고 방문되지 않닸다면 DFS 를 순환호출 해 주면서 방문 해 준다. 이때 정점은 0~size 순으로 루프를 돌기 때문에 숫자가 작은 정점부터 방문되게 된다. *for 문 안에서 재귀를 만나면 바로 DFS 함수로 다시 넘어가 탐색해준다.
DFS 구현 : 인접 리스트
#pragma once
#include "AdjListGraph.h"
#include "CircularQueue.h"
class SrchALGraph : public AdjListGraph
{
bool visited[MAX_VTXS];
public:
void resetVisited() {
for( int i=0 ; i<size ; i++ )
visited[i] = false;
}
bool isLinked(int u, int v) {
for( Node *p=adj[u] ; p!=NULL ; p=p->getLink() )
if( p->getId() == v ) return true;
return false;
}
// 인접 리스트
void DFS( int v) {
visited[v] = true;
printf("%c ", getVertex(v));
for( Node *p=adj[v] ; p!=NULL ; p=p->getLink())
if(visited[p->getId()] == false)
DFS(p->getId());
}
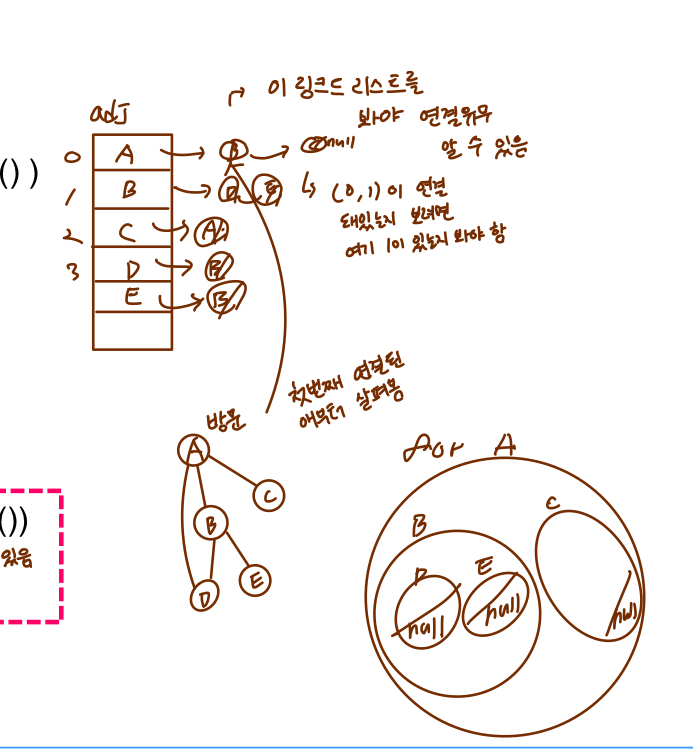
* 인접행렬 결과와 다른다. 인접 리스트의 노드순서는 vertex 인덱스의 역순이기 때문에 ! (head 부분에 노드 삽입)
DFS 분석
-정점 n 개 , 간선 e 개
-인접행렬 O(n^2) , 모든 열 다 확인해야 함
-인접리스트 O(n+e)
-희소 그래프인 경우 DFS 는 인접리스트가 유리하다. (노드가 많은데 엣지가 적은 그래프 )
너비 우선 탐색 (BFS)
BFS : breadth-first search
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어진 정점을 나중에 방문하는 순회 방법
- 큐를 사용하여 구현
- 거리순으로 방문 ( 거리가 0부터 거리가 1인 모든 정점, 거리가 2인 모든 정점 순으로 방문)
BFS 구현 : 인접행렬
// 넓이 우선 탐색 함수
void BFS( int v) {
visited[v] = true;
printf("%c ", getVertex(v));
CircularQueue que;
que.enqueue( v );
while(!que.isEmpty()){
int v = que.dequeue();
for(int w=0; w<size; w++)
if( isLinked(v,w) && visited[w]==false){
visited[w] = true;
printf("%c ", getVertex(w));
que.enqueue(w);
}
}
}
BFS 구현 : 인접리스트
// BFS 인접리스트
void BFS( int v ) {
visited[v] = true;
printf("%c ", getVertex(v));
CircularQueue que;
que.enqueue( v );
while(!que.isEmpty()){
int v = que.dequeue();
for( Node *w=adj[v] ; w!=NULL ; w=w->getLink() ) {
int id = w->getId();
if(!visited[id]){
visited[id] = true;
printf("%c ", getVertex(id));
que.enqueue(id);
}
}
}
}
BFS 분석
- 정점 n 개 , 간선 e개
- 인접행렬 O(n^2)
- 인접리스트 O(n+e)
- 희소 그래프인 경우는 BFS 는 DFS 와 마찬가지로 인접 리스트가 유리
연결 성분
연결성분 ( Connected Components )
- 최대로 연결된 부분 그래프 (떨어져 있는 그래프는 탐색 불가)
연결 성분 구하기
- DFS 또는 BFS 반복 이용 : 임의의 정점에서 탐색을 시작하여 연결돼 있는 보는 정점들을 출력한다. 아직 방문하지 않은 정점을 선택하여 반복한다.
- visited[v] = count 로 교체 1,2 면 true 면서 라벨 표시도 가능하다 !
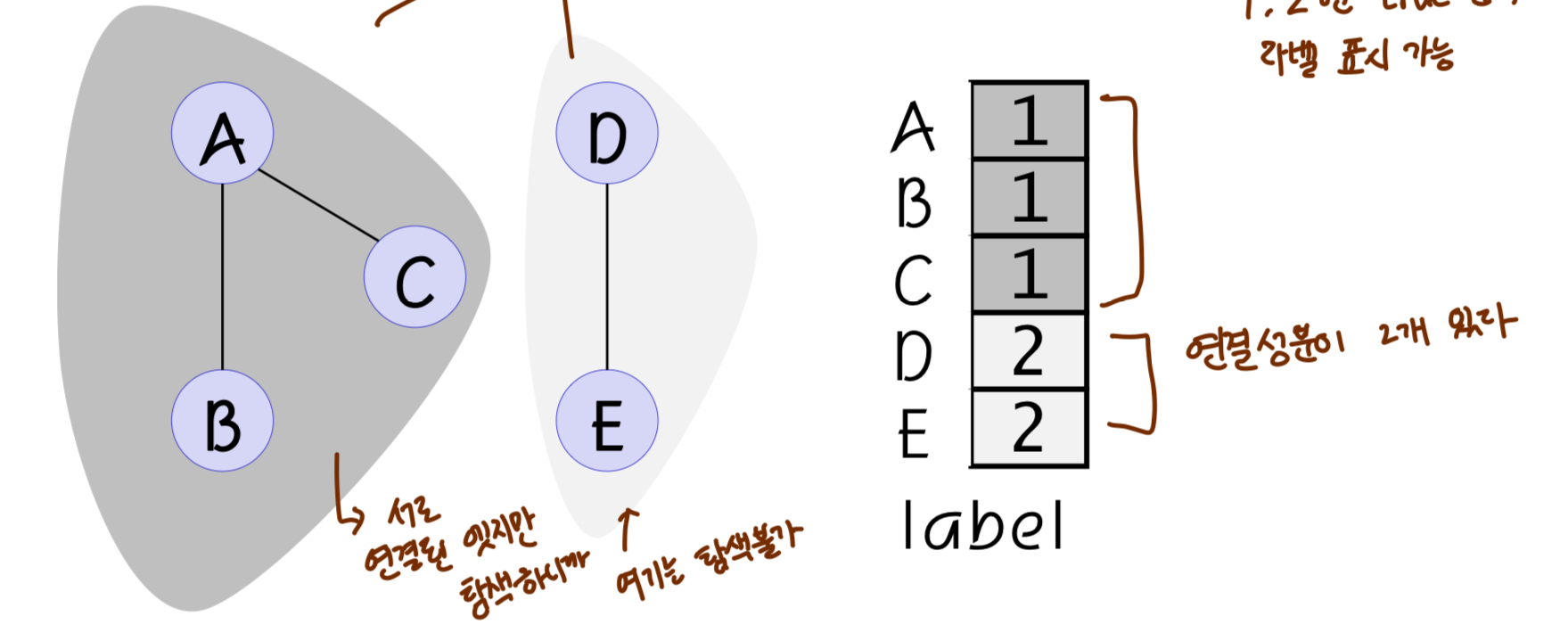
연결성분 코드구현 (인접행렬로 구현)
#pragma once
#include "SrchAMGraph.h"
class ConnectedComponentGraph : public SrchAMGraph
{
int label[MAX_VTXS]; //정점의 색상 필드 추가
public:
void labelDFS( int v, int color) {
visited[v] = true; // 현재 정점을 방문함
label[v] = color; // 현재 정점의 색상
printf("%c ", getVertex(v));
for( int w=0 ; w<size ; w++)
if( isLinked(v,w) && visited[w]==false )
labelDFS( w, color );
}
void findConnectedComponent( ) {
int count = 0;
for(int i=0; i<size ; i++)
if( visited[i]==false){
labelDFS(i, ++count);
}
printf("\n그래프 연결성분 개수 = = %d\n", count);
for( int i=0 ; i<size ; i++ )
printf( "%c=%d ", getVertex(i), label[i] );
printf( "\n" );
}
};