[자료구조] 우선순위큐

알고리즘/자료구조

[자료구조] 우선순위큐

미미_밍 2024. 10. 21. 19:37

큐를 사용하는 예시가 뭐가 있을까 ?

- cpu 의 round Robin 스케쥴링 : cpu 1 개로 여러가지 작업을 한다. 작은 시간을 쪼개면서 큐의 맨 앞에 있는 프로세스를 꺼내고 시간이 끝나면 큐의 마지막을 enque 시켜준다.

* 이때 priority 우선순위가 높은 프로세스는 새치기가 가능하게 구현할 수 있다.

-task 스케쥴링 : task 의 우선순위가 정해져 있다.

우선순위큐

priority queue

- 우선순위를 가진 항목들을 저장하는 큐

- 우선순위가 높은 데이터가 먼저 나가게 된다.(우선순위 값이 미리 정해져 있다. 일반적인 큐가 아니지만 일반적인 큐로 구현은 가능하다.)

- 스택이나 큐를 우선순위 큐로 구현할 수 있다. (늦게들어오면 높은 우선순위 (스택) , 빨리들어오면 높은 우선순위 (큐) )

우선순위큐는 두가지로 구분할 수 있다.

- 최소 우선 순위큐 : 우선순위가 낮은 것부터 삭제

- 최대 우선 순위큐 : 우선순위가 높은 것부터 삭제

우선순위큐 구현방법

1) 배열을 이용한 구현 : 내림차순이든, 오름차순이든 size 알면 젤 큰 값에 바로 접근 가능 O(1)

2) 연결리스트를 이용한 구현 : 내림차순으로 정렬해야 한다. 오름차순이면 리스트 다 뒤져야 젤 큰 노드 찾을 수 있음 O(n)

* insert 시 sorting 되게 하자! 삭제가 빠르게 우선순위 높은게 앞에 오도록

3) 힙 ( heap ) 을 이용한 구현

- 완전 이진트리( complete binary tree )

- 우선순위 큐를 위해 만들어진 자료구조

- 일종의 반 정렬상태 유지 ( sorting 돼 있지만 완전한 sorting 은 아니다 제일 큰 애 뺄 수 있게만 sorting )

힙이란?

heap

- 더미

- 완전 이진트리 (풀 바이너리트리는 완전히 다 차 있어야 , 완전 이진트리는 순서만 맞춰서 채우면 된다.)

- 최대힙, 최소힙 (오름차순이냐 내림차순이냐를 말하는것 )

최대힙

- 부모노드의 키값이 자식 노드의 키값보다 크거나 같은 완전이진트리

최소힙

- 부모노드의 키값이 자식 노드의 키값보다 작거나 같은 완전이진트리

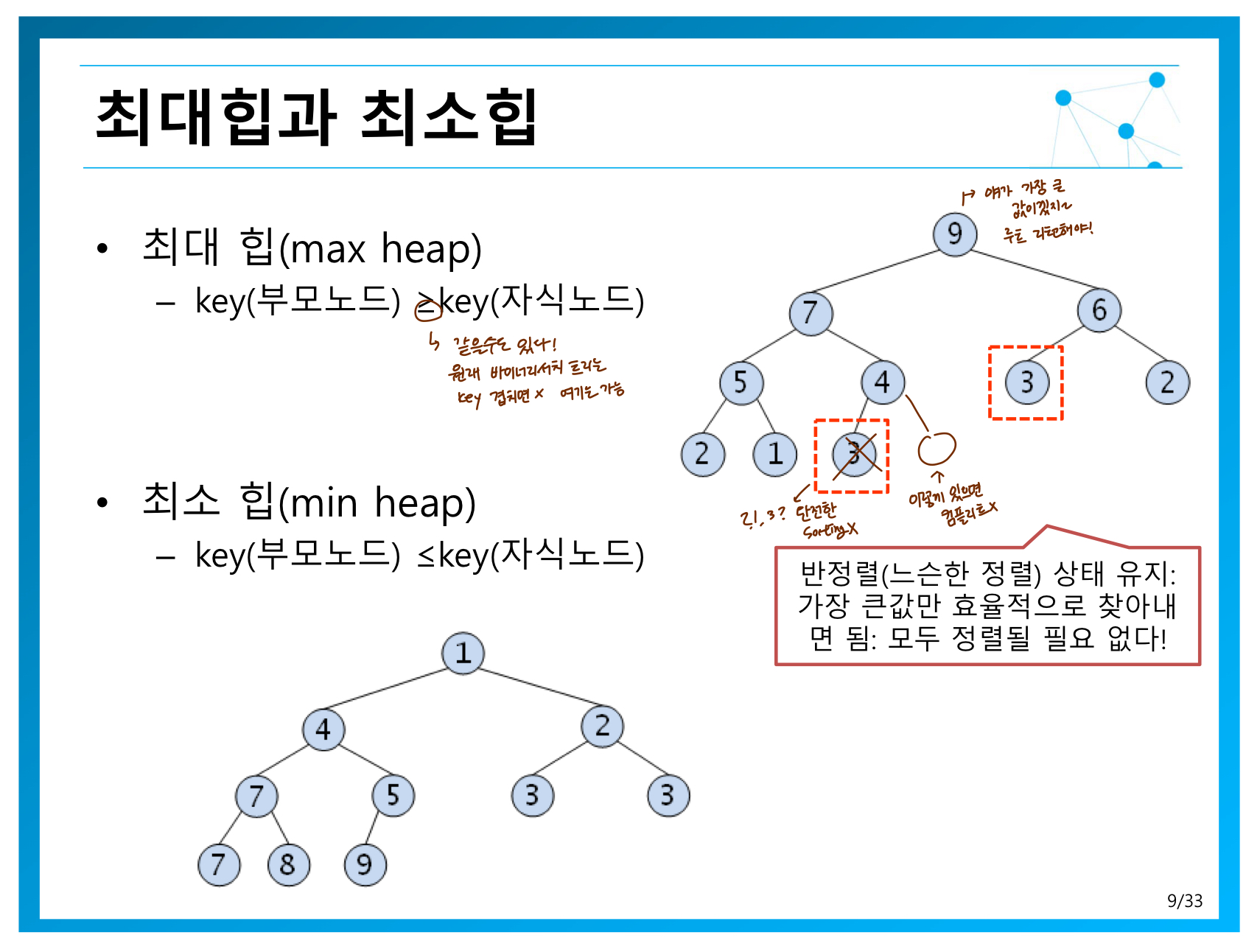
*힙에서는 key 가 중복 될 수 있다.

힙의 높이

n 개의 노드를 가지고 있는 힙의 높이는 O(log2 N)

- 힙은 완전 이진트리

- 마지막 레벨을 제외하고 각 레벨 i 에 2^(i-1) 개의 노드 존재 (완전 이진 트리니까 마지막 레벨은 2의 배수로 안나오겠지 )

힙의 구현 : 배열

힙은 보통 배열을 이용하여 구현

- 완전 이진트리 -> 중간에 빈 노드 없음 -> 각 노드에 번호를 붙임 (인덱스 0은 사용하지 않는다.)

* 보통 인덱스 1 부터 시작하는데 부모-> 자식 노드를 찾아가기 편하게 하기 위해 1 부터 시작한다.

부모노드와 자식노드의 관계

- 왼쪽 자식의 인덱스 = 부모인덱스 * 2 ( 여기서 부모가 0 이 되면 계산이 복잡해 지겠지 ? )

- 오른쪽 자식의 인덱스 = (부모인덱스 *2) +1

- 부모의 인덱스 = 자식으 인덱스/2

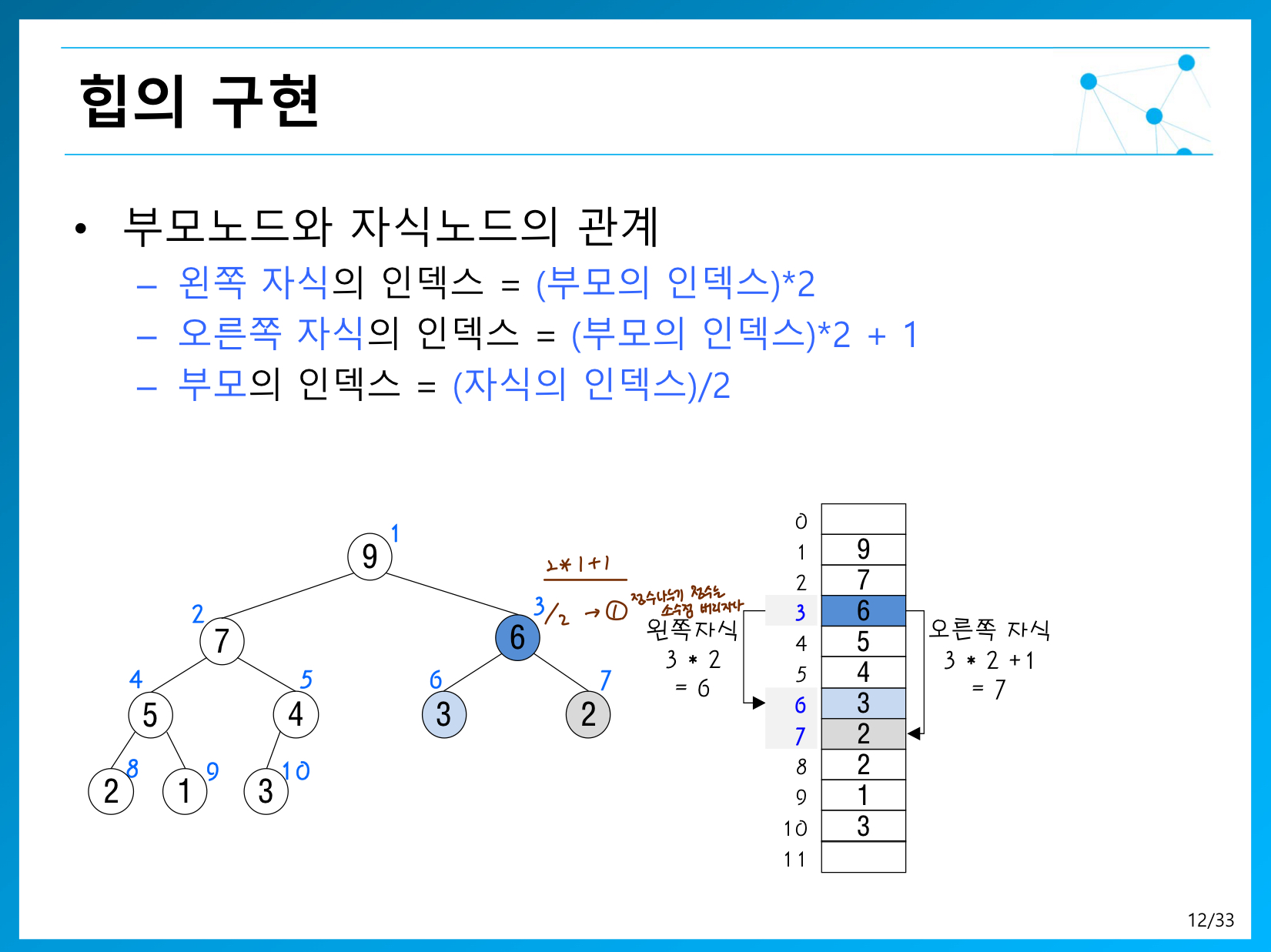
최대힙일 경우 배열을 사용하여 구현 해 보자.

heapNode 객체가 들어가는 배열을 만들어 준다. 배열 size 는 처음 0 부터 insert 할때마다 1 씩 늘어난다.

이때 부모노드, left, right 노드를 구하는 함수는 & 레퍼런스 타입으로 적어주었다. insert 와 remove 는 뒤에서 좀 더 살펴보자.

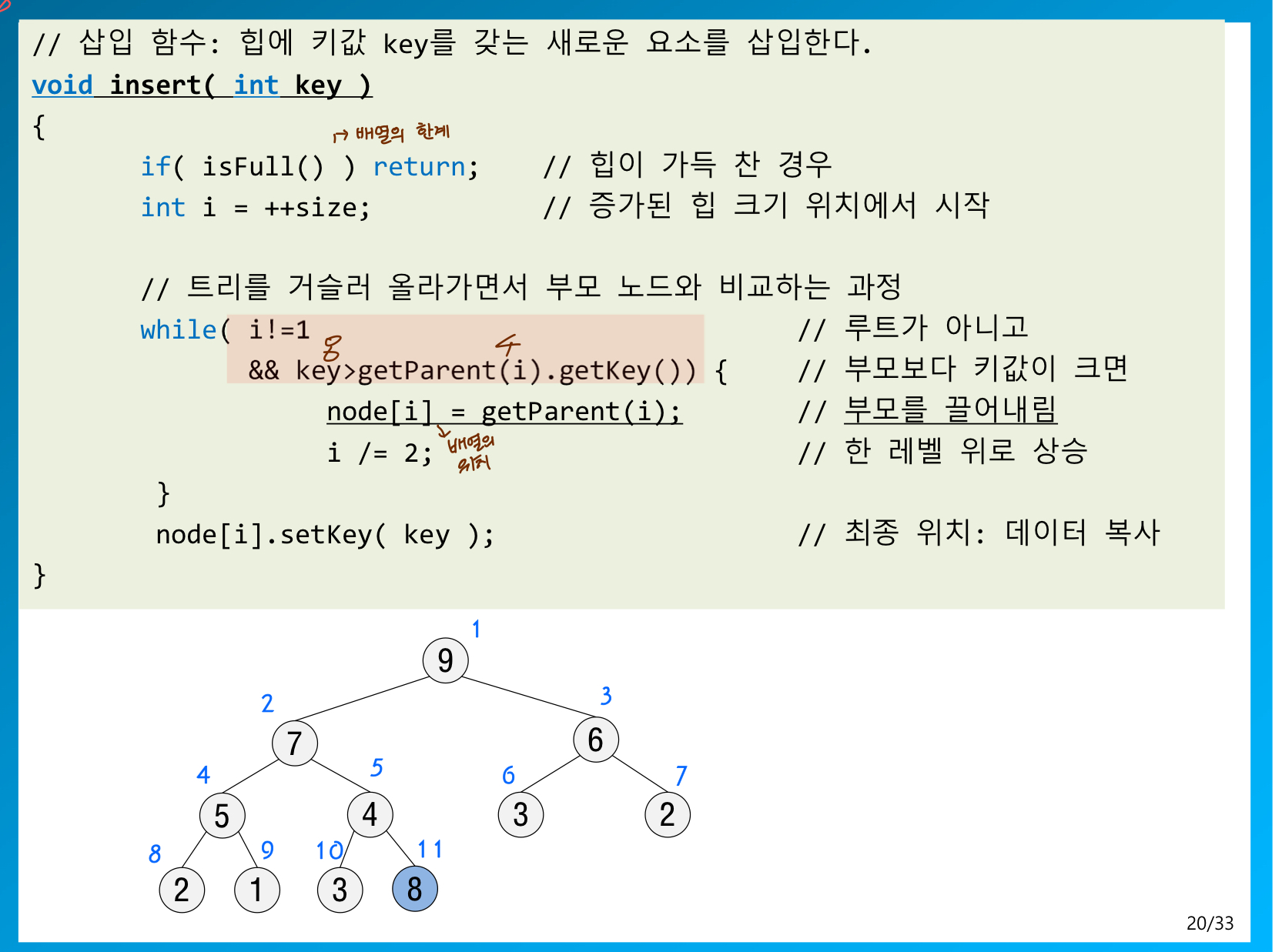
삽입 연산

update

1 ) 힙에 요소가 들어오면 새 노드를 리프노드에 삽입 ( 순서대로! )

2 ) 삽입 후에 새로운 노드를 부모노드들과 교환해서 재정렬

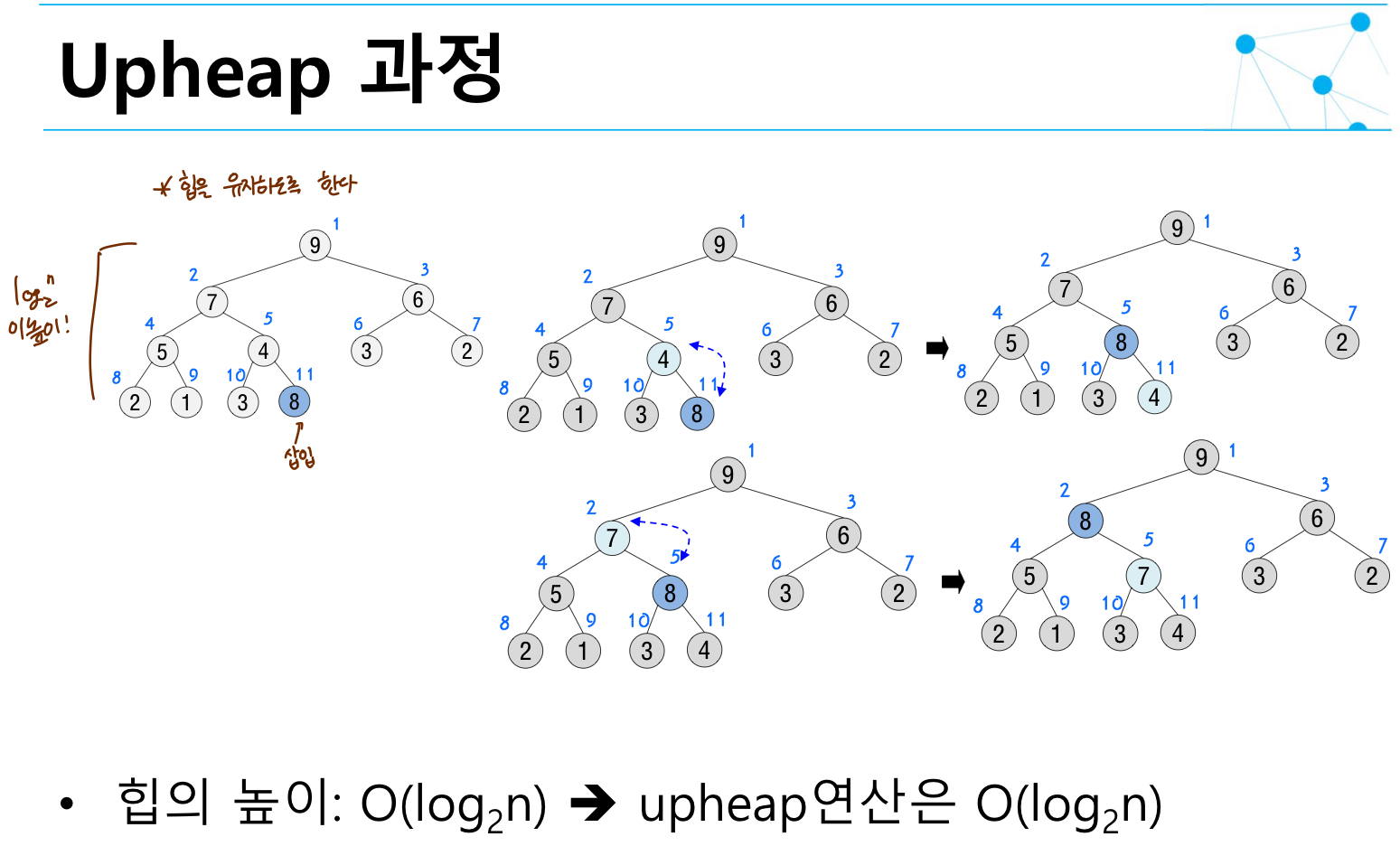
리프노드에서부터 부모노드와 비교해가며 올라간다.

리프노드 즉 i 가 11 일때부터 부모보다 키 값이 큰지 비교하면서 올라간다.

삭제 연산

최대힙에서의 삭제는 항상 루트가 삭제된다.

downheap

-루트삭제

-리프노드를 루트로 올린다.

-루트노드를 자식노드와 비교하면서 재정렬한다.

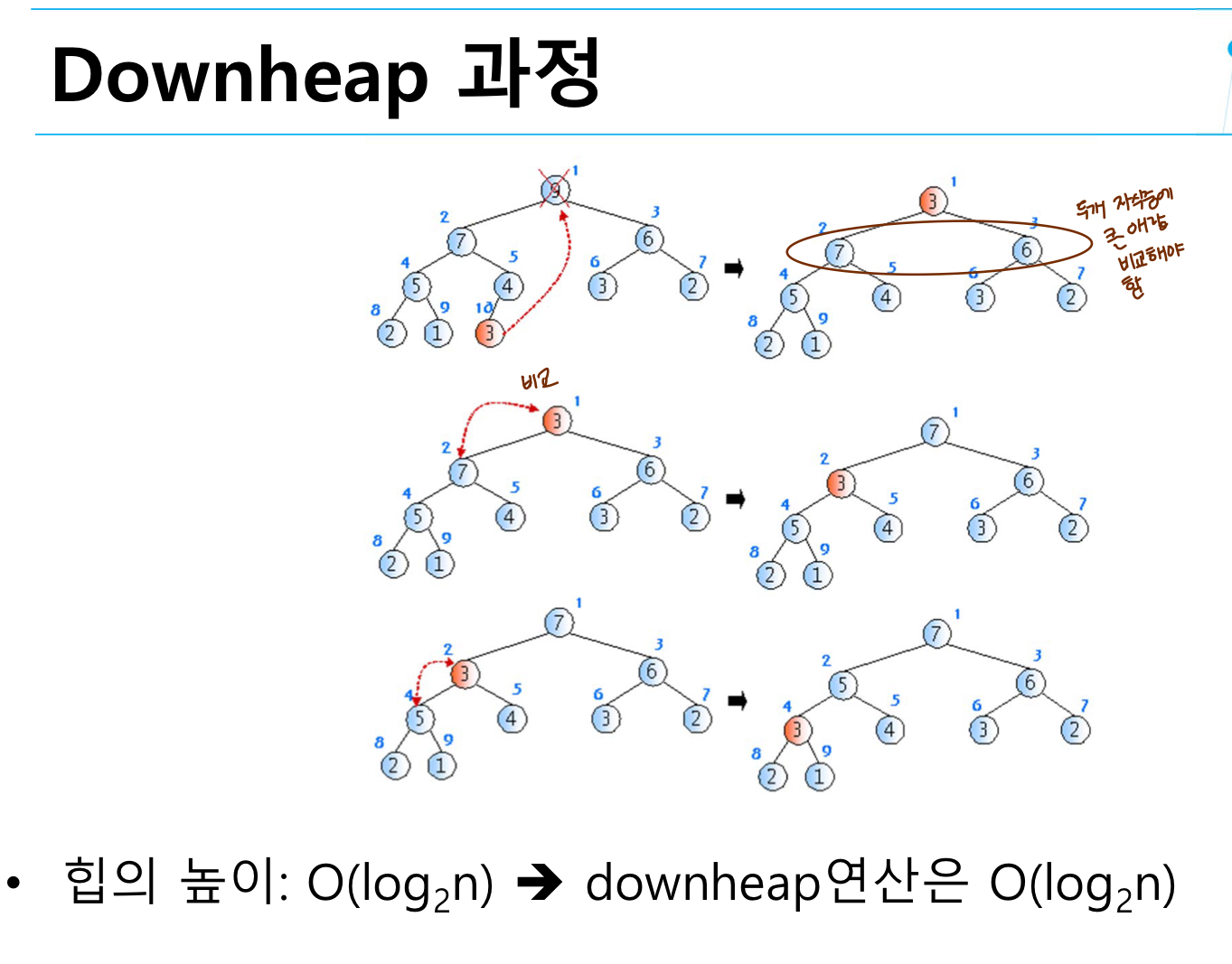
empty 일 경우 에러가 난다. item 에 root 노드 last에 루트노드에 올 노드를 넣고 사이즈를 줄어준다. 루트노드부터 탐색하여 자식의 왼쪽노드보다 오른쪽 노드가 클 경우에 childe 를 증가시켜 오른쪽 노드로 이동 해 준다. ( 배열에 저장되어 있음으로 인덱스 증가 만드로 노드이동이 가능하다. ) 그렇지 않다면 child 를 그대로 2 에 머무르게 한 다음 last 노드 , 루트노드에 올 노드와 선택된 child 의 크기를 비교 해 준다. 만약 last 가 더 크다면 부모노드에 와도 되는 상황임으로 반복문을 멈춰준다. 그게 아니라면 child가 size 보다 클때까지 반복한다. 결국 마지막 노드가 child 보다 커지는 노드를 찾아서 계속 내려오는 것이라 생각하면 된다.

힙의 복잡도 분석

삽입 연산에서 최악의 경우

(루트노드까지 올라가야함 ) O(log2 N)

삭제 연산에서 최악의 경우

(가장 아래 레벨까지 내려가야함) O(log2 N)

=> insert delete 에 좋은 구조

힙 정렬

힙을 이용하면 정렬 가능 : 힙 정렬

- 정렬해야 할 n 개의 요소들을 최대힙에 삽입 (반쯤 정렬)

- 한번에 하나 씩 요소를 힙에서 삭제해서 반환 (remove 하면서 솔팅 하잔슴)

- 삭제되는 요소들은 값이 증가되는 순서 ( 최소힙의 경우 )

시간복잡도

하나 삽입시 : O(log2N)

N개 삽입시 : O(Nlog2 N)

* 전체의 정렬이 아니라 가장 큰 몇 개만 필요할 때 유용

// 힙을 사용한 정렬
inline void heapSort( int a[], int n)
{
	MaxHeap h;
	for(int i=0 ; i<n ; i++ )
		h.insert(a[i]);

	for(int i=n-1 ; i>=0 ;i-- )
		a[i] = h.remove().getKey();
}

힙객체를 선언해주고 받은 사이즈만큼 루프를 돌면서 힙 객체에 a 배열의 값을 넣어준다. ( 숫자로 들어있으며 key 값이 들어온다고 생각한다.)

최대 힙에서는 삭제시 가장 큰 값이 반환됨으로 오름차순으로 정렬하기 위해 a배열의 마지막 부터 시작점까지 remove 의 Return 값을 넣어준다.

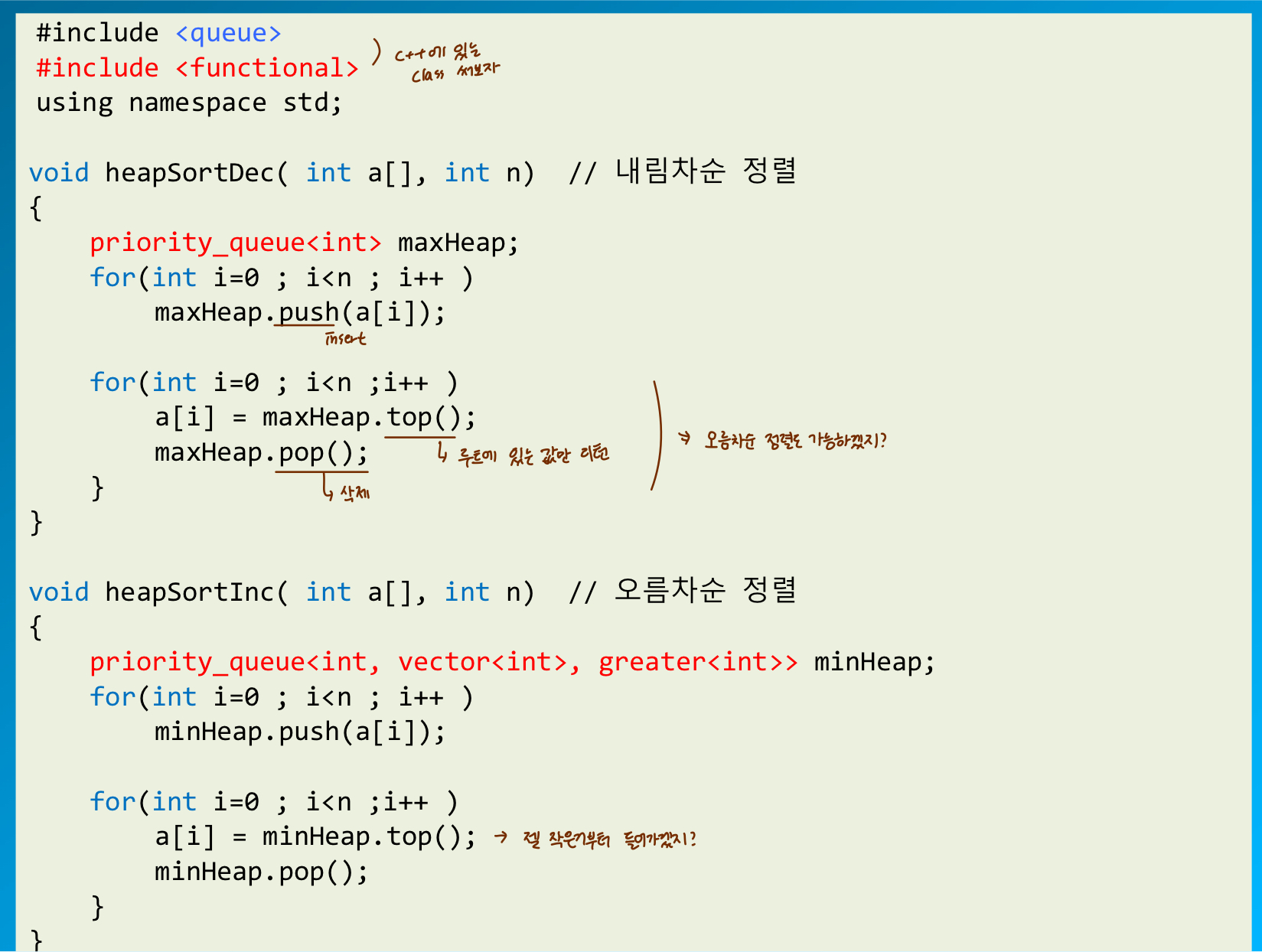
STL 의 우선순위큐

stl 에서도 우선순위큐를 제공한다.

- #include <queue> 헤더파일에 있음

최대힙과 최소힙이 약간 다름

- 최대힙 객체 생성 : priority_queue<int> maxHeap;

- 최소힙 객체 생성 : #include <functional> 추가 , priority_queue<int, vector<int>> minHeap;

허프만 코드

이진 트리는 각 글자의 빈도가 알려져 있는 메세지의 내용을 압축하고 줄이는데 사용될 수 있다.

ex) 허프만 코딩 트리

*많이 나온 글자는 짧은 비트로 코딩하고 작게나온 글자는 긴 비트로 코딩한다.

허프만 코드 생성 절차

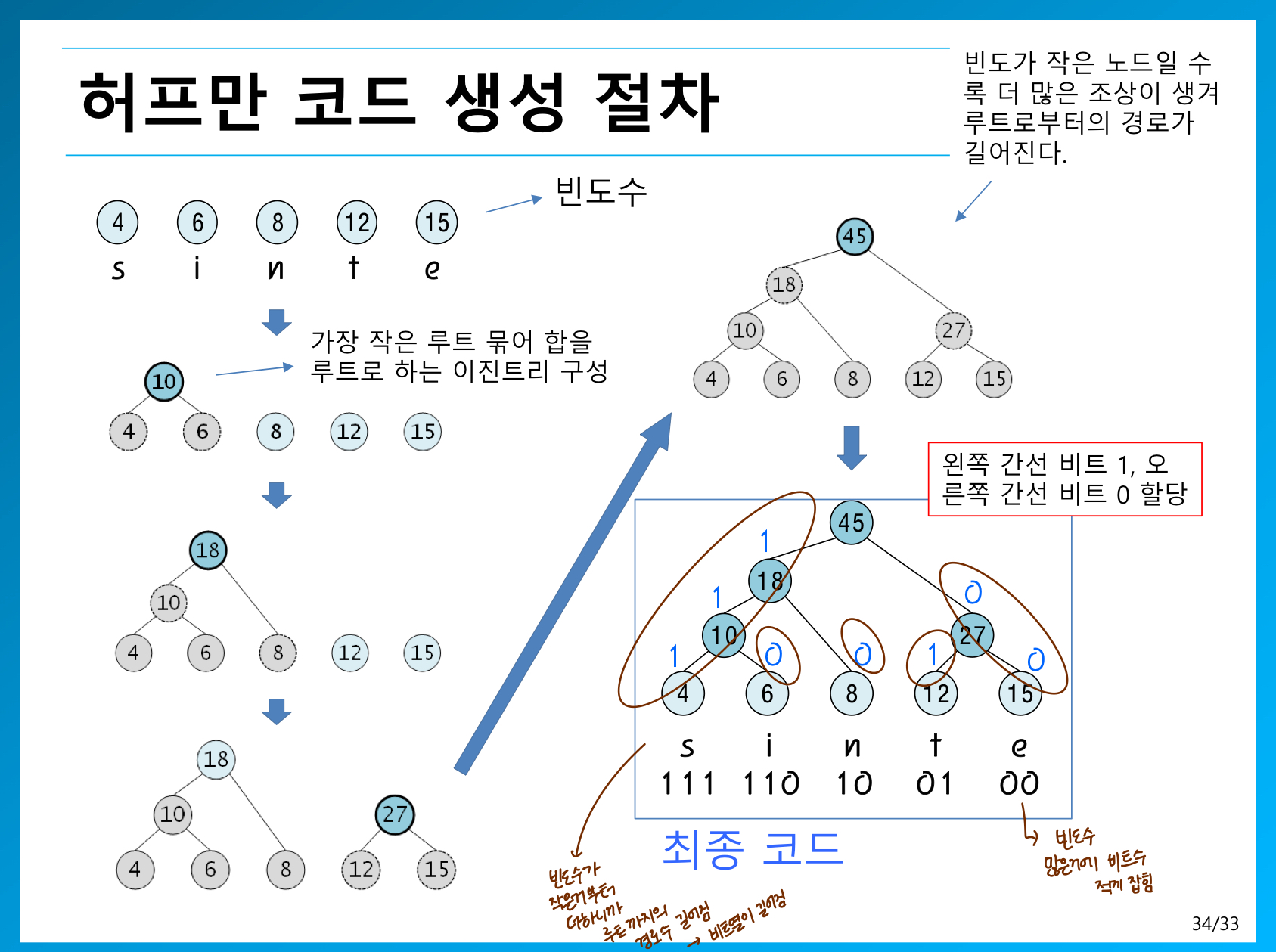
빈도가 작은 노드를 묶어 부모노드를 만든다. 다음으로 빈도가 작은걸 묶어 다시 부모노드를 만들며 해당 작업을 계속 이어간다.

왼쪽 간선은 1 오른쪽 간선은 0 비트를 할당하여 경로가 길어질수록 비트가 많아지도록 구현한다.